- · 《水科学与工程技术》征[05/19]
- · 《水科学与工程技术》投[05/19]
- · 《水科学与工程技术》收[05/19]
- · 《水科学与工程技术》数[05/19]
- · 《水科学与工程技术》栏[05/19]
- · 《水科学与工程技术》刊[05/19]
基于PSO-SVM的来水量预测模型
作者:网站采编关键词:
摘要:降水、气温、径流等多种因子具有很大的不确定性,并影响着中长期的水文预报情况。来水量在年际间具有较大的随机性和不确定性,在影响来水量的众多因素之间也存在着复杂关系,
降水、气温、径流等多种因子具有很大的不确定性,并影响着中长期的水文预报情况。来水量在年际间具有较大的随机性和不确定性,在影响来水量的众多因素之间也存在着复杂关系,众多因素之间的相互作用关系很难利用常规方法进行比较准确的表达。本文通过来水量模型的建立,利用某河45年的径流资料对来年来水量进行预测,并与实际值进行比较。
六是通过论坛、问答社区推广。论坛、问答社区是目前互联网上最有影响力的一个话题产生源,在吸引特定旅游人群方面具有很好的效果[2]。
1 来水量SVM模型
来水量预测模型是反应影响来水量的因素与来水量之间的关系。本文采用用于非线性建模与预测的支持向量回归机模型。
以来水量预测模型为例,模型训练输入为影响因素。由影响因素对应的来水量得到一组输入信号:来水量数据集(X,Y),即:
式中 xi∈Rn为输入向量;yi∈Rn为与xi相对应的输出向量;N为数据点总数。
为了做好技术服务,天脊集团广招贤才,近几年为销售团队来补充了大量新鲜血液。“我们从农业类大学招聘了40多位本科生、研究生。他们有很扎实的理论基础,结合我们的理念,每天到田间地头去给农民服务,让我们的产品在农民那里体现价值,这就是我们现在转型的方向。”
采用某河流45年径流资料对模型进行实例验证,根据水库前期径流资料预测未来年份的来水量。
式中 y为输出向量;x为输入向量;w,b为函数常数项。
芒沙村由于受气候降水和地形的影响,可以充分利用当地的水资源建设水电站。根据南马河流域水利资源在芒沙开发了第一、二级电站,过去没有电站的时候,村里地处低处的水引不上来,后来拦坝,将南马河的水引入,低处的水才得以利用。
假设在ε精度,所有训练样本可用线性拟合函数表示,如式(3):
式中 ε 为精度;其他字母含义同上。
优化目标是最小化‖w‖2/2。由于允许误差,引入松弛变量ξ≥0和 ≥0,如式(4):
≥0,如式(4):
式中 ![]() 分别为松弛变量;其他字母含义同上。
分别为松弛变量;其他字母含义同上。
式(4)中,优化目标是最小化![]()
![]() 常数C>0,C为超出误差 ε 样本的惩罚程度。其对偶问题可利用优化方法,如式(5):
常数C>0,C为超出误差 ε 样本的惩罚程度。其对偶问题可利用优化方法,如式(5):
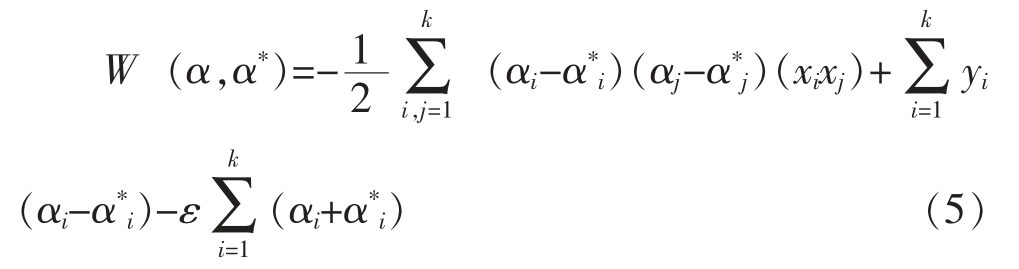
令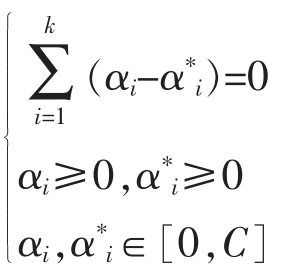
W(α,α*)最大时,由此得到支持向量机的拟合函数[2]f(x),如式(6):
式中 W(α,α*)为目标函数;C为大于零的常数;αi,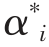 为Lagrange乘子,αi,
为Lagrange乘子,αi,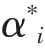 将只有小部分不为0,对应的样本即为支持向量;其他字母含义同上。
将只有小部分不为0,对应的样本即为支持向量;其他字母含义同上。
考虑到非线性问题可通过变换将问题映射到某个高维的特征空间进行求解。用核函数可代替线性问题的内积运算,即K(xi,xj)=φ(xi)φ(xj)。由此,式(5)变换如式(7):
旅游业非正规部门是指在旅游政府部门有效控制以外的和旅游相关的活动。自我就业者他们一般以个人或家庭为经营单位,小规模经营,自产自销,从事的行业不需要较高的技术,具有劳动密集型的特点。他们没有统一组织,散处各地,可与旅游正规部门并存于中心城市,亦可分散于城郊景点,接待对象以本国普通大众游客为主。由于投入少成本低,提供的服务具有低质低价的特点。如销售旅游纪念品的小贩、小手工艺人、人力车司机、无证导游、无营业执照的家庭旅馆和路边的小吃摊。
令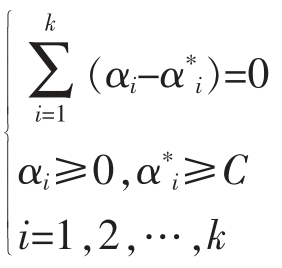
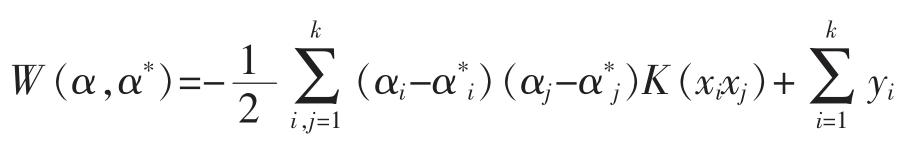
2.1.1 色谱条件色谱柱:Ecosil C18(250 mm×4.6 mm,5 μm);流动相:0.2%甲酸溶液(A)-乙腈(B),梯度洗脱(洗脱程序见表2);流速:1.0 mL/min;柱温:25 ℃;进样量:10 μL。
根据中国合格评定国家认可委员会(CNAS)的要求,专业技术人员中具有中级以上(含中级)专业技术职称或同等能力人员的比例应不少于30%。从表2可看出,广西8家地市级食品药品检验所专业技术人员的职称主要以中级和初级及以下为主,其中有6家机构初级及以下专业技术人员比例高于30%;高级职称专业技术人员占比较低。
本文所用为径向基型,如式(9):
式中 K(x,xi)为核函数;其他字母含义同上。
那么式(6)拟合函数可变换如式(8):
式中 σ 为核函数的宽度;其他字母含义同上。
式中 字母含义同上。
以上为来水量预测的LS-SVM模型。
模型数据从资料的样本集中选取45个数据,其中25个数据作为训练样本,10个数据作为校验样本数据,剩余10个数据作为测试样本数据。设粒子群规模为45,SVM参数C的取值范围 [0.1,104],σ 的取值范围[10-3,10],设最大迭代次数Gmax为500,加速因子c1为0.01,c2为0.01。目标函数为训练样本集和校验样本集的均方差之和为最小,经过PSO优化选择得到使得目标函数最小的最优解C为2816,σ 为1.27。适应度值的迭代优化过程如图1。
2 基于PSO的来水量模型SVM参数优化
粒子群优化算法PSO,是在人类对鸟类捕食时行为研究的基础上得到的一种进化计算方法。由于粒子群算法容易实现且不需要调整过多参数因而被广泛应用于多种领域。
通过输入向量与输出向量的点集进行函数回归[1],如式(2):
彼时许世友担任胶东军区游击队司令员,听说宫宝田就在自己的防区内,便登门拜访。《威海人物》记载:“抗日战争时期,转战胶东的八路军将领许世友曾亲往青山村登门拜会宫宝田,两人言谈甚欢,引为知己。”
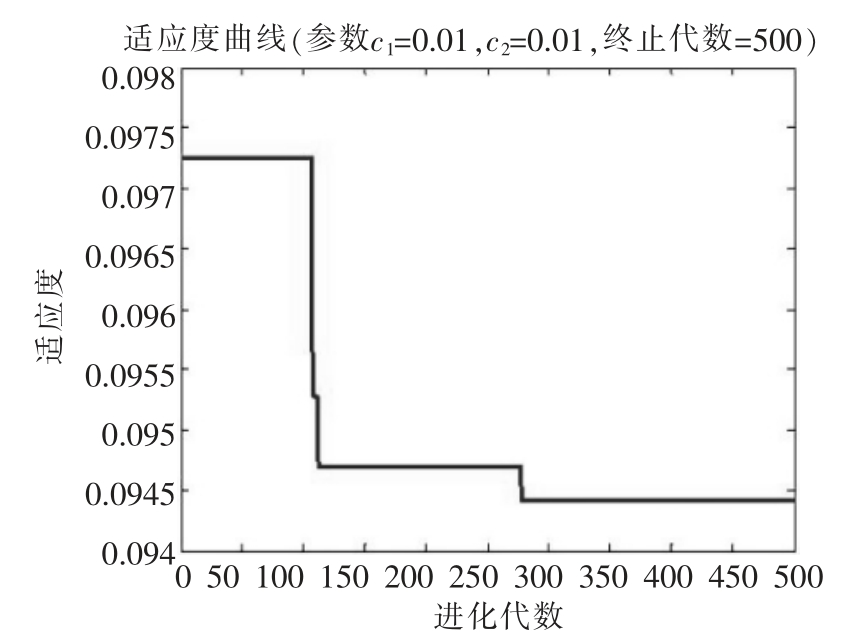
图1 适应度函数进化过程
由图1可见,在100代左右快速收敛,275代左右达到最优值。在最优参数的基础上,模型对10个测试样本数据进行测试,所得预测模型如图2。
当下计算机对于财务管理工作的影响越来越深,财务工作也有很大一部分是依赖于计算机完成的,计算机软件的进步也使得企业的管理与经营更加方便,管理更加有序且成系统,同时也大幅度提高了工作的效率和质量,这就要求着财务人员不能仅仅满足于手头的财务核算工作财务,还要有着一定的综合分析能力以及系统性的管理思维,可以看到数据背后所隐藏的财务信息和价值,能够看到其对企业的意义,为企业日后的经营提供有效判断。仅仅是尽兴核算的传统会计已然不满足当下的时代要求,企业应当积极的将财务会计转型为管理会计,这是必要而且必然的发展趋势。

图2 PSO-SVM预测模型
将模型所得预测值与实际值进行比较,所得误差结果如表1。
表1 PSO-SVM预测结果

编号 实际值 预测值 相对误差/% 均方差1 6 8 7 6 6 4 5 8 -6.0 8 2 5 4 5 3 5 5 6 7 -2.0 9 3 4 5 6 8 4 8 7 4 -6.7 0 4 7 4 0 0 7 5 3 9 -1.8 8 5 8 2 6 6 8 4 5 9 -2.3 3 6 5 5 7 1 5 2 8 9 -5.0 6 7 5 9 7 5 6 0 0 7 -0.5 4 8 4 7 4 3 5 1 0 3 -7.5 9 9 5 8 7 7 5 8 8 0 -0.0 5 1 0 5 9 8 7 5 9 0 1 -1.4 4 4.2 5
实际值与预测值的相对误差绝对值最大值7.59,最小值0.05,均方差4.25。
3 模型比较
本文用相同数据建立BP神经网络模型与PSOSVM模型数据进行比较,BP神经网络预测模型[3]如图3,预测值与实际值的比较如表2。
政府会计制度改革是一个必然过程,在经济和社会发展的推动下,改革措施更适合当前的体制。虽然机构计费系统仍然存在,但随着社会经济的发展,在社会福利机构各部门的共同努力下,会计制度改革将会更加完善。现代事业单位会计制度增强了事业单位会计的资产管理能力,适应了制度的发展,同时也适应了社会的发展。
表2 BP神经网络预测结果

编号 实际值 预测值 相对误差/% 均方差1 6 8 7 6 6 3 3 5 -7.8 7 2 5 4 5 3 5 9 3 3 8.8 0 3 4 5 6 8 5 3 4 5 1 7.0 1 4 7 4 0 0 6 4 9 3 -1 2.2 6 5 8 2 6 6 8 1 5 0 -1.4 0 6 5 5 7 1 5 0 6 1 -9.1 5 7 5 9 7 5 6 0 7 2 1.6 2 8.3 6
续表2

编号 实际值 预测值 相对误差/% 均方差8 4 7 4 3 4 9 2 5 3.8 4 9 5 8 7 7 5 6 7 7 -3.4 0 1 0 5 9 8 7 5 8 4 3 -2.4 1 8.3 6
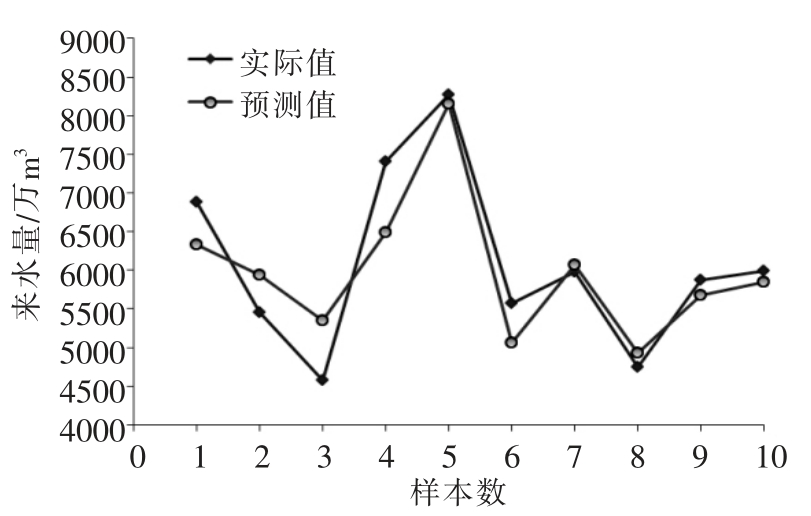
图3 BP神经网络预测模型
BP神经网络模型所得预测值与实际值相对误差的绝对值最大17.01%,最小1.40%,均方差8.36。
从两种模型的预测曲线拟合程度来看,PSOSVM模型拟合程度明显好于BP神经网络模型;从表中的数据分析结果来看,PSO-SVM模型的预测值与实际值的误差的均方差小于BP神经网络预测模型值;PSO-SVM模型对来水量的预测精度更高。
4 结语
建立了来水量PSO-SVM模型,并利用样本数据进行了训练与预测,并利用BP神经网络模型对同一组数据进行了预测,模型数据结果分析表明:PSOSVM模型预测值与实际值的均方差小于BP神经网络,PSO-SVM对预测曲线的拟合程度高于BP神经网络。PSO-SVM模型能够为来水量的预测提供更为精准的参考依据。
[1]王龙强,郄志红,吴鑫淼.冬小麦水肥生产函数的PSO-SVM模型[J].节水灌溉,2013(12):1-4.
[2]王聪聪.基于最小二乘支持向量机的水库来水量预测模型[J].水电能源科学,2014,30(5):29-30.
[3]严阔.基于BP神经网络的来水量预测模型[J].水科学与工程技术,2014(6):43-46.
[4]陶猛.小波神经网络改进算法在来水量预测中的应用[J].节水灌溉,2014(10):38-40.
[5]李楠楠,供水管网爆管故障诊断的PSO-SVM方法[J].系统工程理论与实践,2012,32(9):2014-2010.
Prediction model of inflow based on PSO-SVM
文章来源:《水科学与工程技术》 网址: http://www.skxygcjs.cn/qikandaodu/2020/0519/365.html
上一篇:预制波浪桩在堤防加固工程中的应用
下一篇:观音阁水库超蓄临时淹没损失估算与补偿方案