- · 《水科学与工程技术》征[05/19]
- · 《水科学与工程技术》投[05/19]
- · 《水科学与工程技术》收[05/19]
- · 《水科学与工程技术》数[05/19]
- · 《水科学与工程技术》栏[05/19]
- · 《水科学与工程技术》刊[05/19]
有限元极限平衡法与强度折减法在边坡稳定性分
作者:网站采编关键词:
摘要:我国是一个多山的国家,每年滑坡等地质灾害频发,由此而导致的损失十分严重。在进行滑坡灾害治理时,合理的边坡稳定性评价十分重要。 目前边坡稳定性分析方法主要有2类。第一
我国是一个多山的国家,每年滑坡等地质灾害频发,由此而导致的损失十分严重。在进行滑坡灾害治理时,合理的边坡稳定性评价十分重要。
目前边坡稳定性分析方法主要有2类。第一类为极限平衡法,代表性的有瑞典法[1]、Bishop法[2]、不平衡推力法[3]、摩根斯坦-普莱斯方法[4]等,这些方法能较快地给出边坡的稳定安全系数,比较受工程师青睐。第二类方法为有限元法,包括有限元强度折减法[5]及有限元极限平衡[6],这两类方法在相同边坡模型中的计算精度还缺乏系统研究。
本文基于有限元极限平衡法和强度折减法,重点对比分析澳大利亚计算机应用协会(ACACD)所使用的边坡稳定性考题,用于定量评价这两种有限元法的计算精度。研究结果对提高边坡稳定性的计算精度具有重要意义。
1 基本原理
1.1 有限元极限平衡法
有限元极限平衡法是有限元与极限平衡两种方法的结合。该方法在分析边坡稳定性时,首先利用有限元静力分析求得边坡内的应力应变分布,然后将计算结果通过应力张量变换,求出土条底部的应力,最后根据极限平衡法求得边坡的安全系数。对平面应变问题,首先根据有限元法求得应力场,而后根据摩尔-库伦准则求得相应条块底部的抗剪强度,如图1。
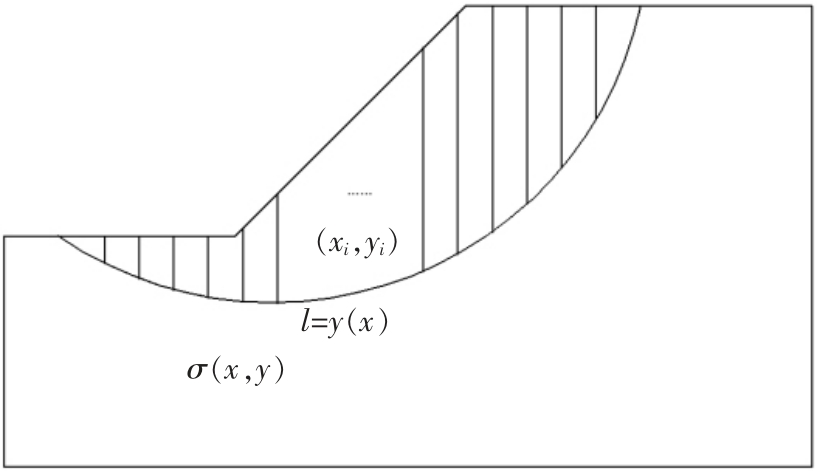
图1 有限元极限平衡法土条受力
假定曲线l为任意一条滑动面,l的方程为l=y(x),则此时边坡的安全系数定义为:
一含软弱夹层的边坡,其几何模型如图4,材料特性参数如表5。
1.2 有限元强度折减法
采用Midas GTS NX分析边坡的稳定性,有限元的网格尺寸大小为0.5m,计算模型采用莫尔-库伦模型。边坡稳定性计算结果如表4。

2 算例分析
本文采用澳大利亚计算机应用协会(ACADS)所采用的边坡稳定性考题[8]对有限元极限平衡法及强度折减法的计算精度进行验证。
2.1 算例1
在酸奶、Mozzarella干酪的发酵过程中、混合菌株间的共生作用让蛋白水解以促进菌株的生长;由图2可知:试验采用传统发酵菌嗜热链球菌、瑞士乳杆菌及筛选的高产抗氧化肽菌株副干酪按不同比例进行复配,发现1∶1∶2的比率能有效促进山羊乳蛋白水解且具有较强的抗氧化活力。
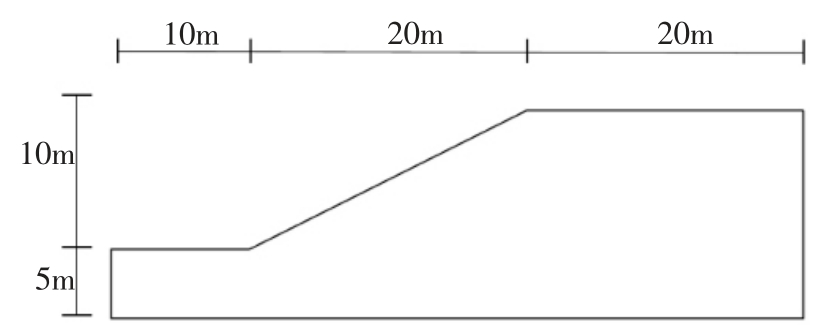
图2 边坡几何模型
表1 算例1边坡土体参数

φ/(°) γ/(kN/m3) E/MPa v c/kPa 3.0 19.6 20.0 10 0.25
在进行小型农田水利工程建设质量的优化时,现行水利行政管理部门应针对整个工程的建设环节进行全方位的统筹管理,并科学合理地配置相关资源。在责任划分时,严格按照施工标准及规范内容执行,借以提升项目工程的监督管理力度,为工程的质量提供保障。另一方面,进行小型农田水利工程的建设管理时,应采用专业水平高超的施工技术进行工程后期的施工质量审计验收,并对后续的工程维护工作进行科学指导,借以有效降低工程管理中各类问题出现的概率。
表2 边坡稳定性计算结果

计算方法 安全系数有限元强度折减法 1.081有限元极限平衡法 1.013 Bishop法 0.993 Janbu法 0.978
从表2可看出,对于均质边坡,有限元强度折减法计算所得的安全系数比有限元极限平衡法的稍大。有限元极限平衡法与Bishop及Janbu法相比,边坡稳定安全系数分别增大2.0%,3.6%;有限元强度折减法与Bishop及Janbu法相比,边坡稳定安全系数分别增大8.8%,10.5%。
2.2 算例2
一多层土边坡,其几何模型如图3,材料特性参数如表3。
本文采用Midas GTS NX分析边坡稳定性,有限元的网格尺寸大小为0.5m,计算模型采用摩尔-库伦模型。边坡稳定性计算结果如表2。
一均质边坡,其几何模型如图2,材料特性参数如表1。
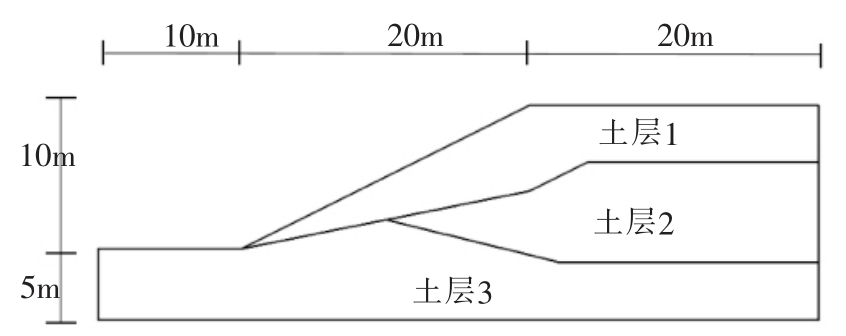
图3 边坡几何模型
表3 边坡土体参数

土层 c/kPa φ/(°) γ/(kN/m3) E/MPa v 1 0 38.0 19.5 10 0.25 2 5.3 23.0 19.5 10 0.25 3 7.2 20.0 19.5 10 0.25
有限元强度折减法中边坡稳定的安全系数定义为:使边坡刚好达到临界状态时,对岩、土体的抗剪强度进行折减的程度[7]。该方法的基本原理是将边坡土体强度参数黏聚力c和内摩擦角φ同时除以一个折减系数F,得到一组新的强度参数,再进行试算,直至边坡达到极限平衡状态为止,此时对应的折减系数F,即为边坡的安全系数。经过折减后,边坡土体的强度参数c′和φ′,如式(2),式(3):
表4 算例2边坡稳定性计算结果

计算方法 安全系数有限元强度折减法 1.450有限元极限平衡法 1.383 Bishop法 1.390 Janbu法 1.325
从表6可看出,对于含软弱夹层边坡,有限元强度折减法与其他方法计算所得的安全系数差别较大,该方法计算所得的安全系数明显偏小,此时边坡等效塑性应变云图如图5,从图5可见边坡的潜在滑动面穿过软弱夹层。有限元极限平衡法与Bishop及Janbu法计算所得的安全系数比较接近。
2.3 算例3
式中 τf为沿滑动面的抗剪强度;τ为沿滑动面的剪应力。
这么勤劳勇敢的爸爸,童年时也会犯全天下小孩都爱犯的毛病——好吃。有次在饭桌上,妈妈无意中说起了爸爸小时的一桩往事。那时正是饥荒年代,家里没饭吃,奶奶好不容易找来一些干枯的红薯藤磨成粉,做成黑漆漆的团子。这样的团子有什么好吃的?可爸爸就是要吃。那时候家里的口粮都是要优先给大人吃的,吃了以后好有力气干活,爷爷见爸爸这样不听话,就提着他浸到水里,谁知爸爸一从水面浮出头,还是哭着说:“我要吃团子!”如此浸了几次,不管他怎么哭,团子还是没吃着。

图4 边坡几何模型
表5 边坡土体参数
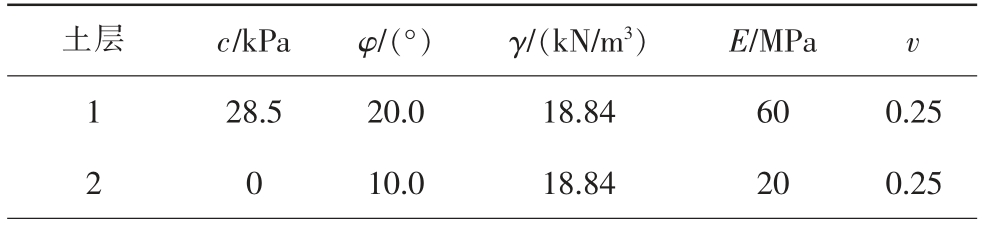
土层 c/kPa φ/(°) γ/(kN/m3) E/MPa v 1 28.5 20.0 18.84 60 0.25 2 0 10.0 18.84 20 0.25
本文采用Midas GTS NX分析边坡的稳定性,有限元的网格尺寸大小为0.5m,计算模型采用莫尔-库伦模型。边坡稳定性计算结果如表6。
表6 边坡稳定性计算结果

计算方法 安全系数有限元强度折减法 1.295有限元极限平衡法 1.600 Bishop法 1.520 Janbu法 1.510
从表4可看出,对于多层土边坡,有限元强度折减法计算所得的安全系数大于有限元极限平衡法计算所得。有限元极限平衡法与Bishop法相比,边坡稳定安全系数减小了0.5%,与Janbu法相比,安全系数增大了4.4%; 有限元强度折减法与Bishop及Janbu法相比,边坡稳定安全系数分别增大4.3%,9.4%。
英格曼神甫和法比·阿多那多并肩走到门前,打开窥探的小窗口,这回小窗口没有伸进一把刺刀,而是一团火红。英格曼看清了,少佐左手将一盆圣诞红举向小窗,右手握在指挥刀把上。
摄影的情况是,歧义的坍缩常常借助于——有时是不恰当地受制于——标题,文字试图解决不确定性,告诉我们薛定谔的猫到底是死是活,却不管正确与否。(没有这些说明,基于照片所显示的证据,猫很可能被认为是睡着了以及/或者死了,如量子一般。)标题是为了将照片限定在单一的状态里,而非开启意义的扩展。如果一张照片被认为值得用一千个词来说明,在标题告诉读者这张照片所谓的内容之后,通常人们不会记得多少。[1]190

图5 基于强度折减法的边坡等效塑性应变云图
为了验证此时有限元强度折减法计算所得结果的合理性,采用极限分析程序Optum G2对算例3进行稳定性计算,计算时采用强度折减极限分析法,计算所得的边坡下限安全系数为1.251,上限安全系数为1.295,可见采用Midas GTS NX中的强度折减法分析所得边坡稳定安全系数的结果是合理的。
3 结语
(1)对于均质及多层土边坡,有限元极限平衡法与强度折减法的计算结果较为接近,两种计算方法与Bishop及Janbu法的误差在10%以内。
阔叶杂草 播娘蒿、荠菜:吡氟酰草胺、二甲四氯、唑草酮、灭草松、双氟磺草胺、苯磺隆、异丙隆、吡草醚;猪殃殃:唑草酮、双氟·唑嘧胺、吡氟酰草胺、吡草醚、双氟+氯氟吡氧乙酸;麦家公:灭草松、双氟磺草胺、苯磺隆、二甲四氯;婆婆纳:唑草酮、吡氟酰草胺+双氟;泽漆:氯氟吡氧乙酸、氯吡+苯磺隆+唑草酮;牛繁缕:二甲四氯、氯氟吡氧乙酸+苯磺隆、吡氟酰草胺、甲基二磺隆、双氟+氟氯酯;佛座:氯氟吡氧乙酸、唑草酮、二甲四氯、氟噻草胺;小蓟:灭草松、二甲四氯;小藜:唑草酮、二甲四氯;麦瓶草:苯磺隆、双氟磺草胺、二甲四氯;紫堇:唑草酮、氯氟吡氧乙酸。
(2)对于含软弱夹层的边坡,有限元强度折减法计算所得的安全系数明显偏小; 而有限元极限平衡法与Bishop及Janbu法计算结果较为接近。
[1]杨剑,蒋国勇,王新军.瑞典条分法与毕肖普法在土坡稳定分析中的应用和研究[J].盐城工学院学报(自然科学版),2005,18(2):66-68.
[2]Bishop A W.The use of the slip circle in the stability analysis of slopes[J].Geotechnique,1995,15(1):62-65.
[3]时卫民,郑颖人,唐伯明,张鲁渝.边坡稳定不平衡推力法的精度分析及其使用条件 [J].岩土工程学报,2004,26(3):313-317.
[4]Chen Z,Morgenstern N R..Extensions to the generalized method of slices for stability analysis [J].Canadian Geotechnical Journal,1983,20(1):104-109.
[5]赵尚毅,郑颖人,时卫民,王敬林.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.
[6]沈保根,黄涛.基于有限元极限平衡法的斜坡式护岸稳定性分析[J].水运工程,2018(7):119-124.
[7]刘顺青,洪宝宁,徐奋强,程涛.高液限土边坡稳定性影响因素的敏感性研究[J].防灾减灾工程学报,2014,34(5):589-596.
[8]陈祖煜.土质边坡稳定性分析——原理·方法·程序[M].北京:中国水利水电出版社,2008.
Comparative study on finite element limit equilibrium method and strength reduction method for the slope stability analysis
文章来源:《水科学与工程技术》 网址: http://www.skxygcjs.cn/qikandaodu/2020/0519/379.html